The above (unfortunately blurry) photo of a blackboard at the IHES was taken during the last of Dennis Gaitsgory’s lectures on Singular support of coherent sheaves, which served as an introduction to his work with Arinkin on the geometric Langlands correspondence over algebraic curves. The blackboard indicates expectations for a local version of the correspondence. It is well understood that the global geometric correspondence should be formulated as an equivalence of categories, but as a matter of general principle the local correspondence is one categorical level up. The top left corner is the 2-category of categories equipped with an action of (the loop group) G((t)), where G is a reductive algebraic group (over the base field, assumed to be algebraically closed of characteristic zero). That’s the representation-theoretic side. The top right corner is the Galois-theoretic side: the 2-category of sheaves of categories over the derived stack LocSys of local systems on the punctured disk with respect to the Langlands dual group of G.
This is a first approximation to the correspondence, but just as in the global situation, there can be no equivalence between the two sides, because something has to be done to the Galois side to take into account the phenomenon of non-temperedness on the geometric (group-theoretic) side. The second line is a reminder of the substitution made in the global correspondence: instead of the category QCoh of quasi-coherent sheaves on LocSys, one has to introduce a new category, called IndCoh_{Nilp}. This is where one needs to begin to think in terms of ∞-categories, and it explains why I know enough of the language of homotopy theory to recognize some of the words used in nLab. The bottom line moves this up to 2-categories, or rather (∞,2)-categories.
There is not yet a book that does for (∞,2)-categories what Lurie’s book did for (∞,1)-categories. Gaitsgory refused to answer when I asked whether such a book would be twice as long as Lurie’s book, or the square of Lurie’s book, or infinitely longer, but even if there were such a book, serious conceptual obstacles remain before Arinkin and Gaitsgory can define the (∞,2)-category in the lower right corner. The challenge to fans of HOTT/UF is to provide the missing concepts. It is an altogether unfair challenge, because to make any sense of the concepts in question, one has to read hundreds if not thousands of pages by Arinkin and Gaitsgory and their collaborators. But Gaitsgory tells me he has no objection to using HOTT/UF to solve the problem.

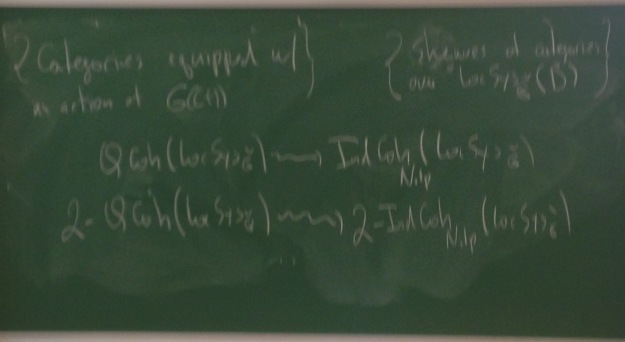
I think the premise of this challenge is misleading. The obstacle to finding the right definition here isn’t due to lacking a basic theory of (infty,2)-categories (such a theory certainly exists, though it is perhaps not as well developed as the (infty,1)-case), it’s due to the fact that we don’t know exactly how a particular example should be defined. (For a very loose analogy, if the Langlands correspondence predicted the existence of a certain Galois representation and we had trouble finding it, I wouldn’t expect that the problem was a failure to understand basic concepts like vector spaces and group actions).
LikeLike
I have to agree with your point, because Dennis said the same thing about the first version of my post. I tried to make the challenge as open-ended as possible, because the precise obstacle is much too technical to describe precisely. The word “conceptual” was meant as a placekeeper to indicate that more is needed than merely (!) a well-developed theory of higher categories, but I agree that it would be natural to read the post in the misleading way you describe.
LikeLike
It’s also unfair because this is not the sort of problem that HoTT/UF has ever been claimed to solve.
LikeLike
I can make Gaitsgory’s point a little clearer (but this is my reconstruction, and not approved). He described the obstacle as one of imagination; he has never encountered a 2-category that does not have a forgetful functor to the 2-category of categories, and the one he needs certainly can’t admit such a forgetful functor. I can easily imagine that such an 2-category would be easier to imagine with different foundations. And it seems to me that this is a problem of a different order than constructing an example.
Since Mike hasn’t been present at all my conversations, he probably doesn’t know the complete list of classes of problems that various people have claimed to be able to simplify using HOTT/UF. But I assume he’s right that those who have been actively involved in developing the theory have never made such claims.
LikeLike
>he has never encountered a 2-category that does not have a forgetful functor to the 2-category of categories, and the one he needs certainly can’t admit such a forgetful functor
this sounds like an analogue of Freyd’s result that the homotopy category of CW-complexes is not concrete.
Though, I would want to clarify if he really means “forgetful functor”, or perhaps something like “global sections”. Regarding the latter, one can for locally small 2-categories (with terminal object, or perhaps some other suitable fixed object) always take Hom(1,-): C -> Cat. Being loose with size, in the absence of a good candidate in place of the terminal object, one could take presheaves of categories over the 2-category and then take global sections.
>problems that various people have claimed to be able to simplify using HOTT/UF.
From my perspective, HoTT/UF qua foundational system really only solves foundational problems. Ordinary mathematics is blind to foundations, and uses things like univalence and proof relevance informally already. The writing down of ZFC didn’t help geometers, PDE experts, algebraic geometers, so what a priori reason do we have to expect a new foundational system will help existing mathematics? The only analogue I can think of for ZFC is issues that set theory touches on in point-set topology or in analysis where subtle points about infinite sets arise (like, for instance l^2(\beta \N)). Likewise, the place where HoTT/UF would make itself felt, if at all, is where homotopy-/higher-category-theoretic aspects raise their head. The example of the Blakers-Massey theorem shows that one might very well be able to compile a HoTT proof down to foundation-agnostic framework (implicitly, naive set theory).
Voevodsky’s stated purpose is machine verification, and good on him. But that’s not HoTT/UF (and he has said that HoTT/UF per the Book is not what he had in mind). Solving the problem of verification/verifiablility is very different to solving the problem of doing the mathematics from scratch.
LikeLike
Nonconcreteness of the homotopy category was the first thing that sprang to my mind too. But I doubt that is the sort of thing being looked for here, since they’re already aiming for the world of (∞,2)-categories.
I would not call naive set theory “foundation-agnostic”. It’s not fully formal, but it nevertheless takes a stand that the basic objects of mathematics, out of which others are built, are sets. HoTT/UF challenges that dogma.
Also, I would warn you to be careful with the use of “HoTT/UF”. I use that combined term when talking about aspects that (I believe) are common to the entire subject. But the phrase “Univalent Foundations” is due to, and closely associated with, Voevodsky, so his interests in machine verification arguably are UF, though they are not as central to HoTT.
LikeLike
@Mike yes, I was a bit unsure about HoTT vs UF vs HoTT/UF. Thanks for clarifying.
Regarding naive set theory, how ‘far’ is it from HoTT/UF, though? Perhaps I should have said instead ‘naive structuralism/set theory’, since some people really do use sets of sets, but nothing that can’t be translated to a structural framework, and thence ‘almost HoTT’.
LikeLike
Naive structural set theory is very similar to the world of hsets inside of HoTT. But there’s a whole universe of n-types above that.
I’m not sure what you mean by “infringing on territory”; we certainly aren’t trying to claim ownership of any part of mathematics. (-:
LikeLike
That said, people who work on homotopy theory using, say, a given model category presentation of an infinity-topos, are obviously infringing on HoTT’s territory, and definitely not using the formalism, so I grant you that one.
LikeLike
@Mike
I said ‘territory’, meaning the raw subject matter (homotopy types), and ‘infringing’ as in touching on, not poaching or trespassing!
Regarding h-sets versus the rest, I guess an example is the contrast VV’s vision of his work done using h-sets (replacing default sets) as opposed to Urs’ vision as trying to do this using the native objects of higher h-levels.
LikeLike
As far as I understand the issue is not a very philosophical one, but rather of the kind that’s extremely common in homotopy theory. One level down, an ind-coherent sheaf is not naturally something like a sheaf of vector spaces with some extra structure, i.e. there’s no natural faithful forgetful functor. So even locally there’s no “underlying vector space”. This is very familiar in the study of Koszul duality — there are chain complexes that are acylic, but which you need to declare nonzero, so if you pass to homotopy too soon you’ll get zero. Of course you can get around this by changing the notion of weak equivalence, but the problem is deeper. This is precisely the same issue as in equivariant homotopy theory, which is defined in terms of diagram categories (like those of Mackey functors) rather than say Borel equivariant homotopy theory which can be described in terms of spaces or spectra with some extra structure. In the ind-coherent setting one can get around this by using the crutch of ind-categories, but really it’s still secretly a diagram category.
One level up the problem is the same, but without the crutch of already knowing the “small” objects concretely: there is no natural “underlying category” or “underlying sheaf of categories” to an object of 2IndCoh, because it is an object of a diagram 2-category, i.e., it’s assembled from a bunch of categories with extra structure glued together. So geometric representation theorists need to learn to think like equivariant homotopy theorists! [In the Betti version of geometric Langlands Nadler and I have such a definition, from talking to Dennis I think the de Rham version will be analogous but harder as one might expect.]
Constantin Teleman’s ICM talk addresses the same issue by the way – if one thinks naively about what “equivariant Fukaya categories” are one runs into contradictions, but he has developed a 2-category of “categories with locally constant G-action” for a compact group G which DOESN’T have an “underlying category” functor (or rather there is one, and it’s zero on many interesting objects).
LikeLike
If diagram categories are what’s at stake, presumably it wouldn’t be such a stretch to think that categorical logic (if not UF) could have at least something to say. The recent ‘Syntactic categories for Nori motives’ by Luca Barbieri-Viale, Olivia Caramello and Laurent Lafforgue (http://arxiv.org/abs/1506.06113) relies heavily on categorical logic.
LikeLike
That’s funny, I was going to make exactly the same suggestion, but I haven’t looked at the paper yet. I am indeed quite interested in Nori motives, for example.
LikeLike
As an outsider, I keep thinking that the answer to all challenges and doubters is for those people who want to do this work to go back to work. You might make a list of challenges and doubts, and put it in a notebook, and perhaps they will be suggestive for where to go next. But the proof of the endeavor is the mathematics you can produce, the theorems and insights and theories you can make, the parts of the world you can illuminate. Now, one is surely entitled to make bets on what is possible in a research program. But in part that depends on the inventiveness and hard work of those who are pursuing it.
I am curious, were there other mathematicians trying to prove the Fermat theorem while Wiles was doing his work? Of course, one the work was made public, a host of mathematicians saw ways of making it clearer and more “efficient.” Namely, to be a first mover is very different than knowing that something actually works and then improving it. Look at what happened when it became known that you could do a good job on the number of paired primes, or the Fundamental Lemma. Maybe others were endeavoring to do that work? I would like to know.
LikeLike
There was at least one other mathematician working on FLT.
LikeLike
It’s worth noting that Wiles didn’t begin working on FLT until Ribet proved that it was implied by the modularity conjecture for elliptic curves. The theory of elliptic curves was very much at the centre of research in number theory, being worked on by the leading experts (including Ribet, of course, and also Mazur, Serre, and many others, Wiles being one of them). I don’t know that anyone besides Wiles really tried to work directly on the modularity conjecture; it had the feel of being out of reach. (And there is no question that Wiles’s proof of it broke down barriers to research, and opened up a flood of research in this direction. To say that other people made Wiles’s proof more “efficient” is a massive understatement of the amount of research, and the progress that has been made, in the direction of modularity following Wiles’s pioneering work.)
On the other hand, the methods that Wiles used: deformations of Galois representations and Galois cohomology, were not created by him out of whole cloth. Mazur introduced the theory of deformations of Galois reps.; he was inspired by Hida’s theory of ordinary families, which (in retrospsect) gave special cases of Mazur’s theory, among other things. Galois cohomology has been a basic tool in algebraic number theory for a century or more. And the Taylor–Wiles method of introducing auxiliary primes was also inspired in part by work of de Shalit, who showed how to make analogues of Hida families by introducing tame, rather than wild, ramification.
This is all to say that Wiles’s work was brilliant, but it took place in the context of a whole community of researchers, and a rich and highly developed thread of research: the theories of modular forms, of elliptic curves, and of Galois cohonmology and Galois representations.
The work on the Fundamental Lemma also took place in a broader context. Waldspurger had done extensive work on the problem, and among other things showed that the function field case implies the number field case (the former being what was eventually proved, but the latter being the case of more interest from the point of view of applications to number theory). Laumon and Ngo together were then able to prove the unitary group case. Finally, Ngo was able to prove the general case. The geometric ideas that he used build on ideas that had been developed over many years by the geometric representation theory community, including Laumon, Ngo himself, and others. Other researchers, e.g. Goresky, Kottwitz, and MacPherson, had previously developed geometric approaches to the fundamental lemma, which ultimately depended on certain purity statements they were unable to prove in general. Ultimately Ngo was able to find a purity statement that he could *prove*, and thus establish the fundamental lemma. But his strategy, and his success, did not take place in a vacuum.
My own view is that very little (maybe no) mathematical research does take place in a vacuum. A view-point that I like (which I learned from my advisor, but which is shared by many people, I would guess including the host of this blog — who also shared the same advisor as me!) is to think of mathematical research as an ongoing conversation between a community of researchers; the problems posed are part of this conversation, as are their solutions. Both problems and solutions are informed by the content and direction of the overall conversation, and in turn influence the way its content and direction develop. And while some conversationalists are more brilliant, and perhaps contribute more, than others, they are all part of the same conversation; they are not in a conversation with themselves.
LikeLike
I was aware of the context for Wiles, and appreciate your explicit statement of that context. I was wondering if anyone else thought they could go forward on FLT at that time. That’s all. The way you present the conversation is that a problem gets worked on in the conversation, and then someone sees a way forward.
LikeLike
With regard to FLT, I have been told that at least one colleague was working in a general way on a proof of modularity of elliptic curves using Galois deformations. This may be the person to whom Als is referring. (I don’t know who Als is, at least not under that name.) I have no reason to believe that Wiles was aware of this other project, which (according to reports) was not close to success when Wiles made his announcement.
LikeLike
The other mathematician tried to use p=2 instead of p=3. Maybe, that would work nowadays (at least if one of the above contributors finished his long and long awaited paper).
LikeLike
Pingback: Various Links | Not Even Wrong
Pingback: How to explain homotopy theory to a number theorist | Mathematics without Apologies, by Michael Harris